Calibration of a catchment using multisite multiobjective composition¶
About this document¶
from swift2.doc_helper import pkg_versions_info
print(pkg_versions_info("This document was generated from a jupyter notebook"))
This document was generated from a jupyter notebook on 2025-11-27 17:28:51.874364
swift2 2.5.6
uchronia 2.6.3
Use case¶
This vignette demonstrates how one can calibrate a catchment using multiple gauging points available within this catchment. This only covers the definition of the calibration, not the execution. The sample data in the package is a small subset of hourly data to keep things (data size, execution time) small.
This is a joint calibration weighing multiple objectives, possibly sourced from different modelling objects in the semi-distributed structure, thus a whole-of-catchment calibration technique. A staged, cascading calibration is supported and described in another vignette.
from swift2.utils import mk_full_data_id
from swift2.classes import CompositeParameteriser, HypercubeParameteriser, Simulation
# from swift2.wrap.ffi_interop import debug_msd
import xarray as xr
import pandas as pd
import numpy as np
import xarray as xr
import swift2.doc_helper as std
import seaborn as sns
import matplotlib.pyplot as plt
from cinterop.timeseries import TIME_DIMNAME, slice_xr_time_series, pd_series_to_xr_series, slice_xr_time_series, pd_series_to_xr_series
from cinterop.timeseries import xr_ts_start, xr_ts_end
import datetime as dt
%matplotlib inline
Data¶
The sample data that comes with the package contains a model definition for the South Esk catchment, including a short subset of the climate and flow record data.
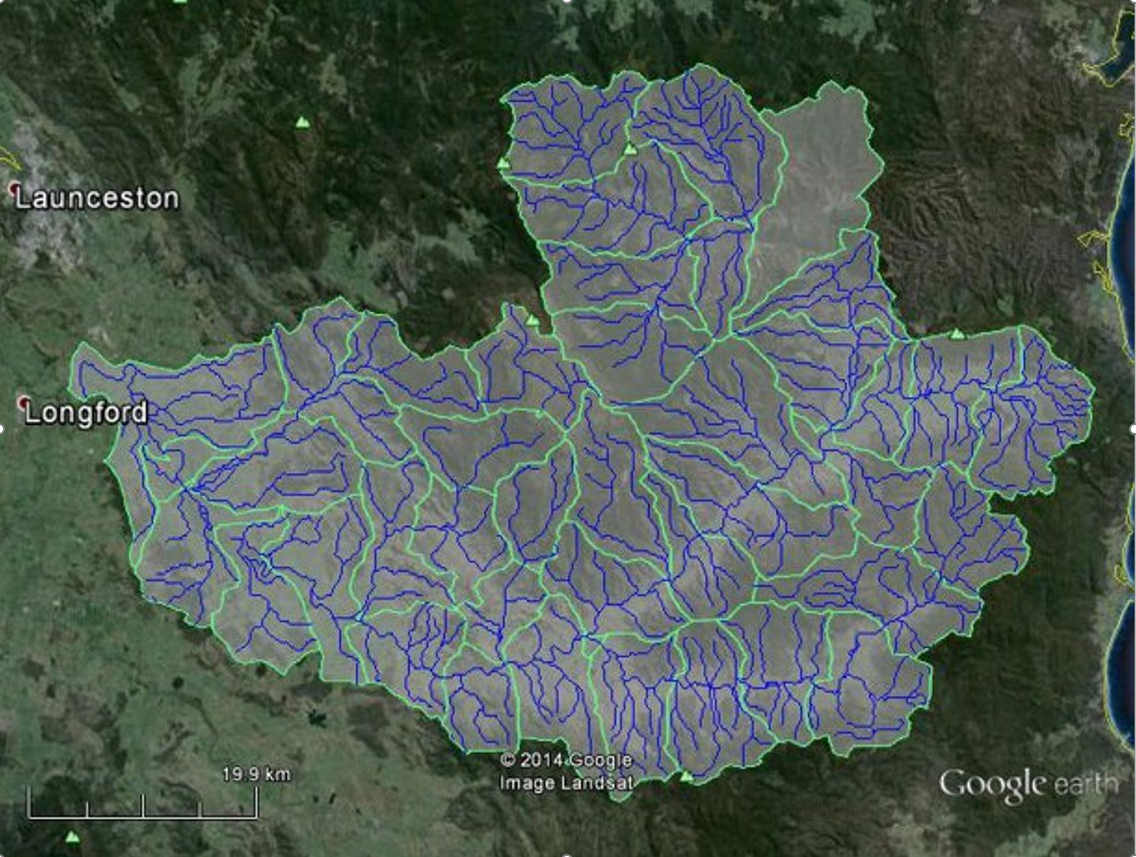
model_id = 'GR4J'
site_id = 'South_Esk'
se_climate = std.sample_series(site_id=site_id, var_name='climate')
se_flows = std.sample_series(site_id=site_id, var_name='flow')
se_climate.head(3)
| subcatchment.1.E | subcatchment.1.P | subcatchment.10.E | subcatchment.10.P | subcatchment.11.E | subcatchment.11.P | subcatchment.12.E | subcatchment.12.P | subcatchment.13.E | subcatchment.13.P | ... | subcatchment.5.E | subcatchment.5.P | subcatchment.6.E | subcatchment.6.P | subcatchment.7.E | subcatchment.7.P | subcatchment.8.E | subcatchment.8.P | subcatchment.9.E | subcatchment.9.P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010-11-01 00:00:00 | 0.3918 | 0.0 | 0.4020 | 0.0000 | 0.3978 | 0.0000 | 0.4266 | 0.0000 | 0.3936 | 0.0000 | ... | 0.4325 | 0.0 | 0.4110 | 0.0322 | 0.4247 | 0.0 | 0.4377 | 0.0 | 0.4337 | 0.0 |
| 2010-11-01 01:00:00 | 0.4385 | 0.0 | 0.4493 | 0.0207 | 0.4446 | 0.0433 | 0.4763 | 0.0179 | 0.4397 | 0.0555 | ... | 0.4823 | 0.0 | 0.4593 | 0.0000 | 0.4746 | 0.0 | 0.4892 | 0.0 | 0.4841 | 0.0 |
| 2010-11-01 02:00:00 | 0.4614 | 0.0 | 0.4723 | 0.0000 | 0.4671 | 0.0000 | 0.5002 | 0.0000 | 0.4619 | 0.0000 | ... | 0.5060 | 0.0 | 0.4827 | 0.0000 | 0.4987 | 0.0 | 0.5143 | 0.0 | 0.5084 | 0.0 |
3 rows × 84 columns
se_climate.tail(3)
| subcatchment.1.E | subcatchment.1.P | subcatchment.10.E | subcatchment.10.P | subcatchment.11.E | subcatchment.11.P | subcatchment.12.E | subcatchment.12.P | subcatchment.13.E | subcatchment.13.P | ... | subcatchment.5.E | subcatchment.5.P | subcatchment.6.E | subcatchment.6.P | subcatchment.7.E | subcatchment.7.P | subcatchment.8.E | subcatchment.8.P | subcatchment.9.E | subcatchment.9.P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2010-11-20 21:00:00 | 0.1832 | 0.0 | 0.1885 | 0.0000 | 0.1865 | 0.0000 | 0.2004 | 0.0 | 0.1844 | 0.0 | ... | 0.2047 | 0.0 | 0.1940 | 0.0 | 0.1988 | 0.0 | 0.2035 | 0.0 | 0.2040 | 0.0 |
| 2010-11-20 22:00:00 | 0.2809 | 0.0 | 0.2877 | 0.1014 | 0.2849 | 0.0289 | 0.3054 | 0.0 | 0.2814 | 0.0 | ... | 0.3104 | 0.0 | 0.2961 | 0.0 | 0.3035 | 0.0 | 0.3105 | 0.0 | 0.3098 | 0.0 |
| 2010-11-20 23:00:00 | 0.3683 | 0.0 | 0.3762 | 0.2028 | 0.3727 | 0.0577 | 0.3990 | 0.0 | 0.3678 | 0.0 | ... | 0.4044 | 0.0 | 0.3872 | 0.0 | 0.3968 | 0.0 | 0.4061 | 0.0 | 0.4041 | 0.0 |
3 rows × 84 columns
Base model creation¶
simulation = std.sample_catchment_model(site_id=site_id, config_id='catchment')
# simulation = swap_model(simulation, 'MuskingumNonLinear', 'channel_routing')
simulation = simulation.swap_model('LagAndRoute', 'channel_routing')
The names of the climate series is already set to the climate input identifiers of the model simulation, so setting them as inputs is easy:
simulation.play_input(se_climate)
simulation.set_simulation_span(xr_ts_start(se_climate), xr_ts_end(se_climate))
simulation.set_simulation_time_step('hourly')
Moving on to define the parameters, free or fixed. We will use (for now - may change) the package calibragem, companion to SWIFT.
std.configure_hourly_gr4j(simulation)
Parameterisation¶
We define a function creating a realistic feasible parameter space. The parameteriser is relatively sophisticated, but this is not the main purpose of this vignette, so we do not describe the process about defining and creating parameterisers in gread details.
from swift2.utils import c, paste0, rep
import swift2.parameteriser as sp
import swift2.helpers as hlp
def create_meta_parameteriser(simulation:Simulation, ref_area=250, time_span=3600):
time_span = int(time_span)
parameteriser = std.define_gr4j_scaled_parameter(ref_area, time_span)
# Let's define _S0_ and _R0_ parameters such that for each GR4J model instance, _S = S0 * x1_ and _R = R0 * x3_
p_states = sp.linear_parameteriser(
param_name=c("S0","R0"),
state_name=c("S","R"),
scaling_var_name=c("x1","x3"),
min_p_val=c(0.0,0.0),
max_p_val=c(1.0,1.0),
value=c(0.9,0.9),
selector_type='each subarea')
init_parameteriser = p_states.make_state_init_parameteriser()
parameteriser = sp.concatenate_parameterisers(parameteriser, init_parameteriser)
hlp.lag_and_route_linear_storage_type(simulation)
hlp.set_reach_lengths_lag_n_route(simulation)
lnrp = hlp.parameteriser_lag_and_route()
parameteriser = CompositeParameteriser.concatenate(parameteriser, lnrp, strategy='')
return parameteriser
parameteriser = create_meta_parameteriser(simulation)
We have built a parameteriser for jointly parameterising:
- GR4J parameters in transformed spaces ($log$ and $asinh$)
- GR4J initial soil moisture store conditions ($S_0$ and $R_0$)
- A "lag and route" streamflow routing scheme in transform space.
There is even more happening there, because on top of GR4J parameter transformation we scale some in proportion to catchment area and time step length. But this is besides the point of this vignette: refer for instance to the vignette about tied parameters to know more about parameter transformation and composition of parameterisers.
parameteriser
Name Value Min Max 0 log_x4 0.305422 0.000000 2.380211 1 log_x1 0.506690 0.000000 3.778151 2 log_x3 0.315425 0.000000 3.000000 3 asinh_x2 2.637752 -3.989327 3.989327 4 R0 0.900000 0.000000 1.000000 5 S0 0.900000 0.000000 1.000000 6 alpha 1.000000 0.001000 100.000000 7 inverse_velocity 1.000000 0.001000 100.000000
Let us check that we can apply the parameteriser and use its methods.
parameteriser.set_parameter_value('asinh_x2', 0)
parameteriser.apply_sys_config(simulation)
simulation.exec_simulation()
We are now ready to enter the main topic of this vignette, i.e. setting up a weighted multi-objective for calibration purposes.
Defining weighting multi-objectives¶
The sample gauge data flow contains gauge identifiers as column headers
se_flows.head()
| 3364 | 18311 | 25 | 181 | 93044 | 592002 | 92020 | 92091 | 92106 | |
|---|---|---|---|---|---|---|---|---|---|
| 2010-11-01 00:00:00 | 1.753 | 0.755 | 1.229 | 11.705 | 10.65 | 0.897 | 0.8 | 8.51 | 9.2 |
| 2010-11-01 01:00:00 | 1.755 | 0.753 | 1.259 | 11.656 | 10.59 | 0.897 | 0.8 | 8.34 | 9.2 |
| 2010-11-01 02:00:00 | 1.746 | 0.743 | 1.280 | 11.606 | 10.56 | 0.897 | 0.8 | 8.00 | 9.2 |
| 2010-11-01 03:00:00 | 1.748 | 0.752 | 1.291 | 11.570 | 10.44 | 0.897 | 0.8 | 7.96 | 9.2 |
| 2010-11-01 04:00:00 | 1.735 | 0.737 | 1.296 | 11.528 | 10.35 | 0.897 | 0.8 | 7.96 | 9.2 |
The network of nodes of the simulation is arbitrarily identified with nodes '1' to '43'
simulation.describe()["nodes"].keys()
dict_keys(['1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18', '19', '20', '21', '22', '23', '24', '25', '26', '27', '28', '29', '30', '31', '32', '33', '34', '35', '36', '37', '38', '39', '40', '41', '42', '43'])
We "know" that we can associate the node identifiers 'node.{i}' with gauge identifiers (note to doc maintainers: manually extracted from legacy swiftv1 NodeLink files)
gauges = c( '92106', '592002', '18311', '93044', '25', '181')
node_ids = paste0('node.', c('7', '12', '25', '30', '40', '43'))
# names(gauges) = node_ids
First, let us try the Nash Sutcliffe efficiency, for simplicity (no additional parameters needed). We will set up NSE calculations at two points (nodes) in the catchments. Any model state from a link, node or subarea could be a point for statistics calculation.
The function multi_statistic_definition in the module swift2.statistics is used to create multisite multiobjective definitions.
import swift2.statistics as ssf
ssf.multi_statistic_definition?
span = simulation.get_simulation_span()
span
{'start': datetime.datetime(2010, 11, 1, 0, 0),
'end': datetime.datetime(2010, 11, 20, 23, 0),
'time step': 'hourly'}
s = span['start']
e = span['end']
calibration_points = node_ids[:2]
mvids = mk_full_data_id(calibration_points, 'OutflowRate')
mvids
['node.7.OutflowRate', 'node.12.OutflowRate']
statspec = ssf.multi_statistic_definition(
model_var_ids = mvids,
statistic_ids = rep('nse', 2),
objective_ids = calibration_points,
objective_names = paste0("NSE-", calibration_points),
starts = [s, s + pd.DateOffset(hours=3)],
ends = [e + pd.DateOffset(hours=-4), e + pd.DateOffset(hours=-2)])
We now have our set of statistics defined:
statspec
| ModelVarId | StatisticId | ObjectiveId | ObjectiveName | Start | End | |
|---|---|---|---|---|---|---|
| 0 | node.7.OutflowRate | nse | node.7 | NSE-node.7 | 2010-11-01 00:00:00 | 2010-11-20 19:00:00 |
| 1 | node.12.OutflowRate | nse | node.12 | NSE-node.12 | 2010-11-01 03:00:00 | 2010-11-20 21:00:00 |
To create a multisite objective evaluator we need to use the create_multisite_objective method of the simulation object. We have out statistics defined. The method requires observations and weights to give to combine statistics to a single objective.
simulation.create_multisite_objective?
observations = [
se_flows[gauges[0]],
se_flows[gauges[1]]
]
w = {calibration_points[0]: 1.0, calibration_points[1]: 2.0} # weights (internally normalised to a total of 1.0)
w
{'node.7': 1.0, 'node.12': 2.0}
moe = simulation.create_multisite_objective(statspec, observations, w)
moe.get_score(parameteriser)
{'scores': {'MultisiteObjectives': 290.33738106858823},
'sysconfig': Name Value Min Max
0 log_x4 0.305422 0.000000 2.380211
1 log_x1 0.506690 0.000000 3.778151
2 log_x3 0.315425 0.000000 3.000000
3 asinh_x2 0.000000 -3.989327 3.989327
4 R0 0.900000 0.000000 1.000000
5 S0 0.900000 0.000000 1.000000
6 alpha 1.000000 0.001000 100.000000
7 inverse_velocity 1.000000 0.001000 100.000000}
We can get the value of each objective. The two NSE scores below are negative. Note above that the composite objective is positive, i.e. the opposite of the weighted average. This is because the composite objective is always minimisable (as of writing anyway this is a design choice.)
moe.get_scores(parameteriser)
{'node.12': np.float64(-347.3329926657439),
'node.7': np.float64(-176.3461578742768)}
log-likelihood multiple objective¶
Now, let's move on to use log-likelihood instead of NSE. This adds one level of complexity compared to the above. Besides calibrating the hydrologic parameters of GR4J and flow routing, with the Log-Likelihood we introduce a set of parameters $(a, b, m, s, ...)$ for each calibration point. The statistic definition is similar and still straightforward
statspec = ssf.multi_statistic_definition(
model_var_ids = mvids,
statistic_ids = rep('log-likelihood', 2),
objective_ids=calibration_points,
objective_names = paste0("LL-", calibration_points),
starts = rep(span['start'], 2),
ends = rep(span['end'], 2) )
statspec
| ModelVarId | StatisticId | ObjectiveId | ObjectiveName | Start | End | |
|---|---|---|---|---|---|---|
| 0 | node.7.OutflowRate | log-likelihood | node.7 | LL-node.7 | 2010-11-01 | 2010-11-20 23:00:00 |
| 1 | node.12.OutflowRate | log-likelihood | node.12 | LL-node.12 | 2010-11-01 | 2010-11-20 23:00:00 |
But while we can create the calculator, we cannot evaluate it against the sole hydrologic parameters defined in the previous section
obj = simulation.create_multisite_objective(statspec, observations, w)
### This cannot work if the statistic is the log-likelihood:
# obj.get_scores(fp)
If we try to do the above we would end up with an error message 'Mandatory key expected in the dictionary but not found: b'
For this to work we need to include parameters
maxobs = np.max(observations[0].values) # NOTE: np.nan??
censor_threshold = 0.01
censopt = 0.0
calc_m_and_s = 1.0 # i.e. TRUE
# const string LogLikelihoodKeys::KeyAugmentSimulation = "augment_simulation";
# const string LogLikelihoodKeys::KeyExcludeAtTMinusOne = "exclude_t_min_one";
# const string LogLikelihoodKeys::KeyCalculateModelledMAndS = "calc_mod_m_s";
# const string LogLikelihoodKeys::KeyMParMod = "m_par_mod";
# const string LogLikelihoodKeys::KeySParMod = "s_par_mod";
p = sp.create_parameteriser('no apply')
# Note: exampleParameterizer is also available
p.add_to_hypercube(
pd.DataFrame.from_dict( dict(Name=c('b','m','s','a','maxobs','ct', 'censopt', 'calc_mod_m_s'),
Min = c(-30, 0, 1, -30, maxobs, censor_threshold, censopt, calc_m_and_s),
Max = c(0, 0, 1000, 1, maxobs, censor_threshold, censopt, calc_m_and_s),
Value = c(-7, 0, 100, -10, maxobs, censor_threshold, censopt, calc_m_and_s)) ))
p.as_dataframe()
| Name | Value | Min | Max | |
|---|---|---|---|---|
| 0 | b | -7.00 | -30.00 | 0.00 |
| 1 | m | 0.00 | 0.00 | 0.00 |
| 2 | s | 100.00 | 1.00 | 1000.00 |
| 3 | a | -10.00 | -30.00 | 1.00 |
| 4 | maxobs | 22.00 | 22.00 | 22.00 |
| 5 | ct | 0.01 | 0.01 | 0.01 |
| 6 | censopt | 0.00 | 0.00 | 0.00 |
| 7 | calc_mod_m_s | 1.00 | 1.00 | 1.00 |
func_parameterisers = [p, p.clone()] # for the two calib points, NSE has no param here
catchment_pzer = parameteriser
fp = sp.create_multisite_obj_parameteriser(func_parameterisers, calibration_points, prefixes=paste0(calibration_points, '.'), mix_func_parameteriser=None, hydro_parameteriser=catchment_pzer)
fp.as_dataframe()
| Name | Value | Min | Max | |
|---|---|---|---|---|
| 0 | log_x4 | 0.305422 | 0.000000 | 2.380211 |
| 1 | log_x1 | 0.506690 | 0.000000 | 3.778151 |
| 2 | log_x3 | 0.315425 | 0.000000 | 3.000000 |
| 3 | asinh_x2 | 0.000000 | -3.989327 | 3.989327 |
| 4 | R0 | 0.900000 | 0.000000 | 1.000000 |
| 5 | S0 | 0.900000 | 0.000000 | 1.000000 |
| 6 | alpha | 1.000000 | 0.001000 | 100.000000 |
| 7 | inverse_velocity | 1.000000 | 0.001000 | 100.000000 |
| 8 | node.7.b | -7.000000 | -30.000000 | 0.000000 |
| 9 | node.7.m | 0.000000 | 0.000000 | 0.000000 |
| 10 | node.7.s | 100.000000 | 1.000000 | 1000.000000 |
| 11 | node.7.a | -10.000000 | -30.000000 | 1.000000 |
| 12 | node.7.maxobs | 22.000000 | 22.000000 | 22.000000 |
| 13 | node.7.ct | 0.010000 | 0.010000 | 0.010000 |
| 14 | node.7.censopt | 0.000000 | 0.000000 | 0.000000 |
| 15 | node.7.calc_mod_m_s | 1.000000 | 1.000000 | 1.000000 |
| 16 | node.12.b | -7.000000 | -30.000000 | 0.000000 |
| 17 | node.12.m | 0.000000 | 0.000000 | 0.000000 |
| 18 | node.12.s | 100.000000 | 1.000000 | 1000.000000 |
| 19 | node.12.a | -10.000000 | -30.000000 | 1.000000 |
| 20 | node.12.maxobs | 22.000000 | 22.000000 | 22.000000 |
| 21 | node.12.ct | 0.010000 | 0.010000 | 0.010000 |
| 22 | node.12.censopt | 0.000000 | 0.000000 | 0.000000 |
| 23 | node.12.calc_mod_m_s | 1.000000 | 1.000000 | 1.000000 |
moe = obj
To get the overall weighted multiobjective score (for which lower is better)
moe.get_score(fp)
{'scores': {'MultisiteObjectives': 45093.298747974426},
'sysconfig': Name Value Min Max
0 log_x4 0.305422 0.000000 2.380211
1 log_x1 0.506690 0.000000 3.778151
2 log_x3 0.315425 0.000000 3.000000
3 asinh_x2 0.000000 -3.989327 3.989327
4 R0 0.900000 0.000000 1.000000
5 S0 0.900000 0.000000 1.000000
6 alpha 1.000000 0.001000 100.000000
7 inverse_velocity 1.000000 0.001000 100.000000
8 node.7.b -7.000000 -30.000000 0.000000
9 node.7.m 0.000000 0.000000 0.000000
10 node.7.s 100.000000 1.000000 1000.000000
11 node.7.a -10.000000 -30.000000 1.000000
12 node.7.maxobs 22.000000 22.000000 22.000000
13 node.7.ct 0.010000 0.010000 0.010000
14 node.7.censopt 0.000000 0.000000 0.000000
15 node.7.calc_mod_m_s 1.000000 1.000000 1.000000
16 node.12.b -7.000000 -30.000000 0.000000
17 node.12.m 0.000000 0.000000 0.000000
18 node.12.s 100.000000 1.000000 1000.000000
19 node.12.a -10.000000 -30.000000 1.000000
20 node.12.maxobs 22.000000 22.000000 22.000000
21 node.12.ct 0.010000 0.010000 0.010000
22 node.12.censopt 0.000000 0.000000 0.000000
23 node.12.calc_mod_m_s 1.000000 1.000000 1.000000}
To get each individual log-likelihood scores for each gauge:
moe.get_scores(fp)
{'node.12': np.float64(-44776.75651455558),
'node.7': np.float64(-45726.383214812144)}